Moore neighbourhood

From LifeWiki
(Redirected from Moore neighborhood)
Jump to navigation Jump to search
The Moore neighbourhood (blue) of a single cell

The Moore neighbourhood is the set of all cells that are orthogonally or diagonally-adjacent to the region of interest (the region of interest itself may or may not be considered part of the Moore neighbourhood, depending on context). For example, the Moore neighbourhood of a single cell consists of the eight cells immediately surrounding it. This neighbourhood is named after Edward F. Moore, one of the pioneers of cellular automata theory.[1] The Moore neighborhood is the neighbourhood of interest in Conway's Game of Life and all Life-like cellular automata, though there are cellular automata that use other neighbourhoods such as the 4-cell von Neumann neighborhood.

The Moore neighbourhood naturally extends to cellular automata in higher dimensions, for example forming a 26-cell cubic neighborhood for a cellular automaton in three dimensions. The number of cells in the Moore neighbourhood of a single cell in an n-dimensional cellular automaton is 3n - 1 (Sloane's OEISicon light 11px.png A024023).

The Moore neighbourhood of a cell can be thought of as the points at a Chebyshev distance of 1 from that cell.

Generalizations

See also: Isotropic non-totalistic cellular automaton

Like in the hexagonal neighborhood, isotropic cellular automata using the Moore neighbourhood can be defined using Hensel notation, which was devised by Alan Hensel and represents the relative permutations of the cells using letters.

0 1 2 3 4 5 6 7 8
— (no
letter) 		INT Moore R1 0.png INT Moore R1 8.png
c
(corner) 		INT Moore R1 1c.png INT Moore R1 2c.png INT Moore R1 3c.png INT Moore R1 4c.png INT Moore R1 5c.png INT Moore R1 6c.png INT Moore R1 7c.png
e
(edge) 		INT Moore R1 1e.png INT Moore R1 2e.png INT Moore R1 3e.png INT Moore R1 4e.png INT Moore R1 5e.png INT Moore R1 6e.png INT Moore R1 7e.png
k
(knight) 		INT Moore R1 2k.png INT Moore R1 3k.png INT Moore R1 4k.png INT Moore R1 5k.png INT Moore R1 6k.png
a
(adjacent) 		INT Moore R1 2a.png INT Moore R1 3a.png INT Moore R1 4a.png INT Moore R1 5a.png INT Moore R1 6a.png
i INT Moore R1 2i.png INT Moore R1 3i.png INT Moore R1 4i.png INT Moore R1 5i.png INT Moore R1 6i.png
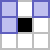n INT Moore R1 2n.png INT Moore R1 3n.png INT Moore R1 4n.png INT Moore R1 5n.png INT Moore R1 6n.png
y INT Moore R1 3y.png INT Moore R1 4y.png INT Moore R1 5y.png
q INT Moore R1 3q.png INT Moore R1 4q.png INT Moore R1 5q.png
j INT Moore R1 3j.png INT Moore R1 4j.png INT Moore R1 5j.png
r INT Moore R1 3r.png INT Moore R1 4r.png INT Moore R1 5r.png
t INT Moore R1 4t.png
w INT Moore R1 4w.png
z INT Moore R1 4z.png

For instance, B2-a/S12 (the Just Friends rule) indicates that a dead cell will be born with 2 neighbors, except when they are adjacent, and that a live cell will survive with 1 or 2 neighbors in any configuration.

Higher ranges

The Moore neighbourhood can also be defined with a higher range; that is, so that it captures cells that are further than one cell away from the region of interest. The standard Moore neighbourhood has range 1. The Moore neighbourhood of range 2 is the set of all cells that are orthogonally or diagonally adjacent to the Moore neighbourhood (of range 1). The Moore neighbourhood of range n can be defined recursively as the set of all cells that are orthogonally or diagonally adjacent to the Moore neighbourhood of range n - 1. The number of cells in the Moore neighbourhood of range n is given by (2 n + 1)2 - 1 (Sloane's OEISicon light 11px.png A033996).

Symmetries

Main article: Static symmetry

The Moore and von Neumann neighbourhoods rely on a different grid than the hexagonal neighbourhood and thus features a different set of inherent symmetries when dealing with isotropic rules:

  • C2_1
  • C2_2
  • C2_4
  • C4_1
  • C4_4
  • D2_+1
  • D2_+2
  • D2_x
  • D4_+1
  • D4_+2
  • D4_+4
  • D4_x1
  • D4_x4
  • D8_1
  • D8_2 (only occasionally preserved)
  • D8_4

Gallery

  • The Moore neighbourhood (blue) of an eater 1

  • The Moore neighbourhood of range 2 of a single cell

  • The Moore neighbourhood of range 3 of a single cell

See also

References

  1. ↑ Tim Tyler. "The Moore neighbourhood". Retrieved on June 13, 2009.

External links

Retrieved from "https://conwaylife.com/w/index.php?title=Moore_neighbourhood&oldid=119158"